Eenheidscel
De eenheidscel is een begrip dat op het grensvlak van de meetkunde en de kristallografie ligt. De eenheidscel wordt in de wiskunde gedefinieerd en aan de hand daarvan in de kristallografie gebruikt, bijvoorbeeld om verschillende kristalstructuren van elkaar te kunnen onderscheiden. Het komt er op neer, dat een eenheidscel in een kristal de kleinst mogelijke basiseenheid is, die, wanneer die in de drie verschillende mogelijke richtingen wordt gekopieerd, de ruimte vult en zo het kristal vormt.
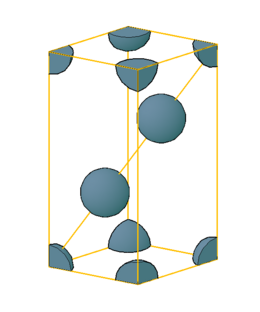


Eenheidscellen vinden hun toepassing in de materiaalkunde en vastestoffysica en het deel van de structuuranalyse, waarbij röntgendiffractie wordt toegepast.
Wiskunde bewerken
Een eenheidscel van een symmetrie die translatiesymmetrie bevat is een fundamenteel domein van alleen de translatiesymmetrie. Dit geldt voor alle mogelijke dimensies.
Ieder kristalrooster bevat per definitie ten minste translatiesymmetrie, dus kan voor ieder kristalrooster een eenheidscel worden gedefinieerd. Een eenheidscel in een kristalrooster in drie dimensies is altijd een parallellepipedum, maar alle verschillende vormen daarvan, de balk, kubus en de romboëder komen ook als eenheidscel voor. De tegenover elkaar liggende zijvlakken van de eenheidscel liggen dus evenwijdig. De eenheidscel van een kristalrooster wordt zo gekozen, dat het de hoogste symmetrie heeft en het volume eventueel zo klein mogelijk is. De eenheidscel is een basiseenheid in het rooster, waaruit het gehele kristal kan worden gedacht te zijn opgebouwd. De eenheidscel bevat een of meer atomen. Ieder atoom heeft een vaste positie binnen de cel, die in relatieve (x,y,z)-coördinaten kan worden uitgedrukt. Het gehele kristal kan door translatie van de eenheidscel in de drie richtingen van het kristallografisch assenstelsel worden opgebouwd, waarbij er geen lege ruimte over blijft.
Alle mogelijke symmetrieën van een gegeven kristalrooster worden bepaald door het bravaisrooster van dat kristalrooster en door de mogelijke kristallografische puntgroepen van de eenheidscellen in het rooster. De combinatie van 14 verschillende bravaisroosters en 32 puntgroepen geven 230 mogelijke ruimtegroepen. Dat zijn er dus minder dan het product , maar dat komt omdat binnen die 448 niet alle combinaties zijn toegestaan en er andere combinaties isomorf zijn.
Het ligt voor de hand om met de eenheidscellen voor driedimensionale kristalroosters te beginnen, maar het is ook mogelijk eenheidscellen voor het platte vlak te bepalen. Er zijn in twee dimensies vier stelsels: het parallellogram, de rechthoek, de ruit en het vierkant en vijf bravaisroosters, omdat er voor de rechthoek een primitieve en een gecentreerde eenheidscel is. De 17 verschillende behangpatroongroepen zijn over deze vijf bravaisroosters verdeeld. Dat betekent dat de eenheidscellen binnen de 17 behangpatroongroepen vijf verschillende vormen hebben.
Kristalstelsels bewerken
De mogelijke vormen van de eenheidscel hangen van het kristalstelsel af waar die eenheidscel een onderdeel van is. De grootte van de cel en de hoeken tussen de assen worden gedefinieerd door de roosterconstanten. De eenvoudigste vorm, die een eenheidscel kan hebben, is de vorm van een kubus. Er zijn veertien manieren, waarop een kristalstructuur meetkundig kan worden beschreven. De Franse kristallograaf Auguste Bravais heeft ze in 1848 beschreven. Ze zijn naar hem de bravaisroosters genoemd.
Eenheidscellen bouwen door translatie in de drie richtingen een rooster op. Noem de lengten van de ribben in de drie richtingen van de eenheidscel en . Er ontstaat op deze manier een rooster door de eenheidscellen over een lengte in de drie verschillende richtingen te transleren, dus over en , maar het kan zich voordoen dat er meer mogelijkheden zijn. Dat hangt van het bravaisrooster af. De 14 mogelijke bravaisroosters zijn in zeven kristalstelsels ingedeeld en zijn behalve door het kristalstelsel door het soort eenheidscel bepaald.
Er volgt in de tabel bij ieder van de vier mogelijke soorten eenheidscellen een voorbeeld. Er staat bij iedere soort eenheidscel de notatie.
- primitieve eenheidscellen P - De hierboven genoemde translaties zijn bij eenheidscellen, die primitief worden genoemd, de enige translaties, waarbij een rooster in zichzelf over gaat.
- ruimtelijk gecentreerd I - Bij ruimtelijk gecentreerde eenheidscellen zijn ook alle translaties van een van de hoekpunten naar het midden van de eenheidscel mogelijk. Van het midden naar een van de hoekpunten is hetzelfde. Het rooster wordt dan toch nog op zichzelf afgebeeld.
- grondvlak gecentreerd S - Het rooster blijft bij grondvlak gecentreerde eenheidscellen hetzelfde onder translaties in twee van de drie richtingen van de hoekpunten naar het midden van een zijvlak hetzelfde.
- vlakken gecentreerd F - Het rooster blijft bij grondvlak gecentreerde eenheidscellen hetzelfde onder de translaties in alle drie de richtingen van de hoekpunten naar het midden van een zijvlak hetzelfde.
| kristalstelsel | primitief | gecentreerd |
|---|---|---|
| kubisch | ||
| monoklien | ||
| orthorombisch |
Dit zijn vier voorbeelden van de 14 bravaisroosters, die er zijn. Er is bij iedere vorm van gecentreerde eenheidscel ook een primitieve eenheidscel, zoals is aangegeven bij het kubische kristalstelsel. De eenheidscel bevat bijvoorbeeld in een kubisch vlakgecentreerd rooster vier atomen, terwijl de primitieve eenheidscel maar één atoom bevat. De eenheidscellen bevatten in een kubisch ruimtelijk gecentreerd rooster twee atomen. De verschillende bravaisroosters worden in de tabel door hun Pearson symbool aangegeven.
Wigner-Seitz-cel bewerken
Een Wigner-Seitz-cel is een speciale vorm van eenheidscel, die dezelfde symmetrie heeft als het kristalrooster. Een Brillouinzone is een Wigner-Seitz-cel in het reciproque rooster.