Sinusoïde
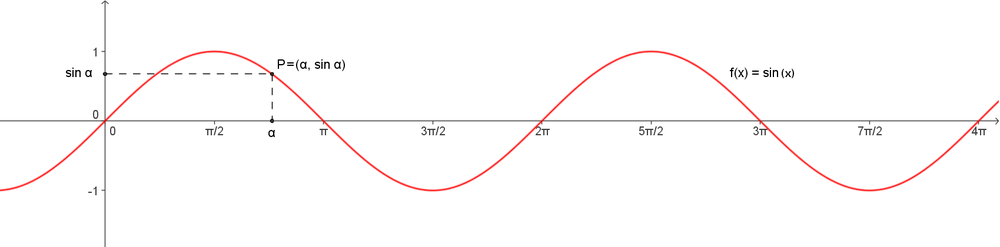
De sinusfunctie en de cosinusfunctie zijn sinusoïden. De grafiek van de sinusoïden zijn de bekende golflijnen. Merk op dat deze functie periodiek is met periode 2π. De sinus heeft dus dezelfde waarde voor de hoeken α, α+2π, α+4π, ... De grafiek is op de intervallen , , enz. een herhaling van het deel tussen 0 en 2π. Dit komt doordat een hoek van bijvoorbeeld 480° = 1×360°+120°, dus een keer helemaal rond en dan nog eens 120°, als echte hoek gelijk is aan een hoek van 120°.
De constructie en eigenschappen van de cosinus zijn analoog.
De sinusoïde is een grafiek die zich gedraagt als een sinus of cosinus. Dit wil zeggen volgens de functie
of
Hierin geldt:
- evenwichtsstand = d
- amplitude = |a|
- periode = 2π/|b|
- verschuiving horizontaal = c
- startpunt in een sinus = (c;d)
NB: de cosinus is dus ook een sinusoïde, want: cos(x) = sin(x - ½π)
Hierna wordt genomen en is de tijd, geschreven .
Sinusoïdale functies van tijd en hun complexe versie bewerken
De algemene vorm van een sinusoïdale functie van tijd is
met de hoekfrequentie, de amplitude en de fase.
Deze functies kunnen 1-op-1 geassocieerd worden met de complexe functies van de tijd
met reële , en die aan dezelfde voorwaarden voldoen als boven, door dezelfde waarden te kiezen.[1] Het reële deel van de complexe functie is . De complexe functie wordt wel de complexe versie van de sinusoïdale functie genoemd.
Dit wordt bijvoorbeeld toegepast in complexe wisselstroomrekening.
De verhouding van de complexe spanning over een component tot de complexe stroomsterkte er doorheen heet de impedantie van de component.
Meer algemeen heet de verhouding van de complexe versie van de sinusoïdale output van een lineair tijdinvariant continu systeem tot de complexe versie van de sinusoïdale input met dezelfde hoekfrequentie de frequentierespons. Deze is afhankelijk van het systeem en van de hoekfrequentie, maar niet van de tijd, en niet van de amplitude en fase van de input. De amplituderespons is de verhouding van de amplitude van de sinusoïdale output tot de amplitude van de sinusoïdale input. Deze is gelijk aan de absolute waarde van de frequentierespons. De faserespons is de fase van de output, verminderd met de fase van de input. Deze is gelijk aan het argument van de frequentierespons (waarbij veelvouden van bij fasen en faseverschillen niet meetellen).
Bij een inputsignaal dat meerdere (hoek)frequenties bevat is de output niet te beschrijven als een verandering van amplitude en fase, doordat de amplitude- en faserespons van de (hoek)frequentie afhangen. Het outputsignaal is daardoor anders van vorm.
Voorbeeld 1 bewerken
Als
en is sinusoïdaal met complexe versie
dan is de sinusoïde met complexe versie
Er geldt dus
Dit kan gebruikt worden om als sinusoïdaal is, de sinusoïde te vinden die een particuliere oplossing is van de lineaire differentiaalvergelijking.
Voorbeeld 2 bewerken
Als
en is sinusoïdaal met complexe versie
dan is de sinusoïde met complexe versie
Er geldt dus
Dit kan gebruikt worden om als sinusoïdaal is, de sinusoïde te vinden die een particuliere oplossing is van de lineaire differentiaalvergelijking.
Voor en geeft dit echter geen oplossing voor Y, omdat er in dit geval geen sinusoïdale oplossing is. Een particuliere oplossing van
is
Dit correspondeert met resonantie bij een ongedempte harmonische oscillator.
Zie ook bewerken
Bronnen, noten en/of referenties
|



![{\displaystyle f(x)=a\sin[b(x-c)]+d}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d6c533fab6113b44bfb9f7941ffcb87607f45e4)
![{\displaystyle f(x)=a\cos[b(x-c)]+d}](https://wikimedia.org/api/rest_v1/media/math/render/svg/005204ff27cce0f0c83ae75e096f8d65c977b874)


