Uniforme verdeling (continu)

De continue uniforme verdeling is een verdeling op een interval met constante kansdichtheid, wat inhoudt dat er geen voorkeur is voor enige waarde uit dat interval. De kansdichtheid $f$ van de uniforme verdeling op het interval $(a,b)$ is daarom constant en wordt gegeven door:

Uniforme verdeling (continu)
Kansdichtheid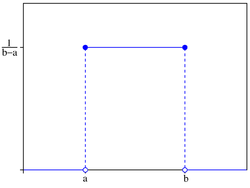
Verdelingsfunctie
Parameters	$a,b\in (-\infty ,\infty )$
Drager	$a\leq x\leq b$
Kansdichtheid	${\begin{cases}{\frac {1}{b-a}}&{\text{voor }}a<x<b\\0&{\text{voor}}\ x\leq a\ {\text{of }}x\geq b\end{cases}}$
Verdelingsfunctie	${\begin{cases}0&{\text{voor }}x<a\\{\frac {x-a}{b-a}}&{\text{voor }}a\leq x<b\\1&{\text{voor }}x\geq b\end{cases}}$
Verwachtingswaarde	${\frac {a+b}{2}}$
Mediaan	${\frac {a+b}{2}}$
Modus	N/A
Variantie	${\frac {(b-a)^{2}}{12}}$
Scheefheid	$0$
Kurtosis	$-{\frac {6}{5}}$
Entropie	$\ln(b-a)$
Moment- genererende functie	${\frac {e^{tb}-e^{ta}}{t(b-a)}}$
Karakteristieke functie	${\frac {e^{itb}-e^{ita}}{it(b-a)}}$
Portaal    Wiskunde

$f(x)={\begin{cases}{\frac {1}{b-a}}&{\text{voor }}a<x<b\\\\0&{\text{elders}}\end{cases}}$

Voor elk deelinterval $(x,x+\Delta )$ met lengte $\Delta$ is de kans op een waarde daaruit $\Delta /(b-a)$.

Opmerking

De uniforme verdeling kan ook beschouwd worden op half open of gesloten intervallen. De functiewaarden van de dichtheid in de eindpunten van het interval doen niet terzake. In alle gevallen is de verdelingsfunctie dezelfde:

$F(x)={\begin{cases}0&{\text{voor }}x<a\\{\frac {x-a}{b-a}}&{\text{voor }}a\leq x<b\\1&{\text{voor }}x\geq b\end{cases}}$

Verwachtingswaarde en variantie

De verwachtingswaarde $\mathrm {E} X$ van een uniform op $(a,b)$ verdeelde stochastische variabele $X$, en de variantie $\mathrm {var} (X)$, worden gegeven door:

$\mathrm {E} X={\frac {a+b}{2}}$

en

$\mathrm {var} (X)={\frac {(b-a)^{2}}{12}}$

Zie ook

• Uniforme verdeling (discreet)

Kansverdelingen