Tetrahedrale en octahedrale symmetrie
Tetrahedrale en octahedrale symmetrie en de bijbehorende pyritohedrale symmetrie omvatten vijf vormen van polyhedrale symmetrie, en wel de symmetrie van onder meer het viervlak of tetraëder en de kubus. Het eerste woord van elke symmetrie wordt ook wel eens zonder h geschreven, met dan de uitgang edrale of edrische, al of niet met trema.
-
chirale tetrahedrale symmetrie T van orde 12
-
pyritohedrale symmetrie Th van orde 24
-
volledige tetrahedrale symmetrie Td van orde 24
-
chirale octahedrale symmetrie O van orde 24
-
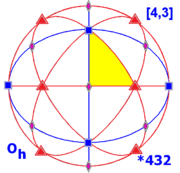
volledige octahedrale symmetrie Oh van orde 48



Deze vijf figuren geven een vooraanzicht van de bol die de symmetrie weergeeft. De rotatie-assen zijn daarbij met de kleine symbolen aangegeven, het fundamentele domein is geel en verbindende grote cirkels geven aan waar de eventuele spiegelvlakken de bol snijden. De figuren zijn in orthografische projectie getekend en tonen dus precies een halfrond. Alle rotatieassen en de aangegeven grote cirkels zijn ook van toepassing op dezelfde plaats aan de achterkant. Merk op dat een ellips geen grote cirkel voorstelt, maar twee halve grote cirkels aan de voorkant van de bol.
Dezelfde symmetrie kan ook op een driehoekige hexaëder of op een kubus worden geprojecteerd. Een driehoekige hexaëder is een catalanlichaam. Alle elementen van de symmetriegroep van de kubus zijn dus tetrahedraal, octahedraal of pyritohedraal.
De symmetrieën in de vijf figuren met een bol hebben gemeen dat ze allemaal vier assen van rotatiesymmetrie van orde 3 hebben. Ze hebben het volgende aantal punten waar ze het oppervlak van een convex object, er is in de afbeeldingen voor een bol gekozen, met de betreffende symmetrie snijden. Het aantal assen is steeds de helft:
- 8 van orde 3. De assen gaan bij de kubus door de hoekpunten. Anders gezegd: de snijpunten met een bol vormen de hoekpunten van een kubus.
- 0 of 6 van orde 4. De assen gaan bij de kubus door de middens van de zijvlakken.
- 6 of 12 van orde 2. De assen gaan bij de kubus door de middens van de ribben.
Th heeft verder nog drie in blauw aangegeven spiegelvlakken, Td zes die in rood zijn aangegeven, en Oh heeft ze allemaal.
De groepen , , , en zijn de symmetriegroepen van de kubus met:
- voor blanco zijden
- voor op elk zijvlak dezelfde chirale figuur met rotatiesymmetrie van orde 4
- voor op elk zijvlak een diagonaal zo dat die samen een tetraëder vormen
- voor op elk zijvlak een lijnstuk dat de middens van twee tegenover elkaar liggende zijden verbindt, zodanig dat zulke lijnstukken elkaar niet raken; ook de symmetriegroep van een pyritoëder
- voor zowel het bij als genoemde
is de symmetrie van het viervlak en een archimedisch lichaam, de afgeknotte tetraëder. is algebraïsch de symmetrische groep , want de elementen van komen 1-op-1 overeen met de permutaties van de 4 hoekpunten.
is algebraïsch de alternerende groep , want de elementen van komen 1-op-1 overeen met de even permutaties van de 4 hoekpunten.
en dus algebraïsch . De groep is niet alleen de chirale versie van maar ook van .
is de symmetrie van de kubus, het regelmatige achtvlak of octaëder en vijf archimedische lichamen. Twee archimedische lichamen, namelijk de beide versies van de stompe kubus, zijn chiraal met als totale symmetriegroep. is algebraïsch de symmetrische groep , waarbij de elementen 1-op-1 overeenkomen met de permutaties van de lichaamsdiagonalen van de kubus,[1] en dus algebraïsch . Behalve zijn ook en , dus , ondergroepen van . De groep is een ondergroep van O.
| Bronnen, noten en/of referenties |